Beaucoup de gens pensent que les mathématiques sont un invention humaine. Pour cette façon de penser, les mathématiques sont comme un langage : elles peuvent décrire des choses réelles dans le monde, mais elles n’existent pas en dehors de l’esprit des personnes qui les utilisent.
Mais l’école de pensée pythagoricienne de la Grèce antique avait un point de vue différent. Ses partisans croyaient que la réalité est fondamentalement mathématique.
Plus de 2000 ans plus tard, les philosophes et les physiciens commencent à prendre cette idée au sérieux.
Comme je l’argumente dans un nouveau papier, les mathématiques sont une composante essentielle de la nature qui structure le monde physique.
Abeilles et hexagones
Les abeilles dans les ruches produisent des nids d’abeilles hexagonaux. Pourquoi?
Selon la « conjecture en nid d’abeille » en mathématiques, les hexagones sont la forme la plus efficace pour carreler l’avion. Si vous souhaitez couvrir entièrement une surface à l’aide de carreaux de forme et de taille uniformes, tout en gardant la longueur totale du périmètre au minimum, les hexagones sont la forme à utiliser.

Le motif hexagonal du nid d’abeilles est le moyen le plus efficace pour couvrir un espace de carreaux identiques. Crédit : Sam Baron
Charles Darwin a raisonné que les abeilles ont évolué pour utiliser cette forme car elle produit les plus grandes cellules pour stocker le miel pour le plus petit apport d’énergie pour produire de la cire.
La conjecture en nid d’abeille a été proposée pour la première fois dans l’Antiquité, mais n’a été prouvé en 1999 par le mathématicien Thomas Hales.
Cigales et nombres premiers
Voici un autre exemple. Il existe deux sous-espèces de cigales périodiques nord-américaines qui vivent la majeure partie de leur vie dans le sol. Puis, tous les 13 ou 17 ans (selon les sous-espèces), les cigales émergent en grands essaims pendant une période d’environ deux semaines.
Pourquoi est-ce 13 et 17 ans? Pourquoi pas 12 et 14 ans ? Ou 16 et 18 ans ?
Une explication fait appel au fait que 13 et 17 sont des nombres premiers.

Certaines cigales ont évolué pour émerger du sol à des intervalles d’un nombre important d’années, peut-être pour éviter les prédateurs avec des cycles de vie de différentes longueurs.
Imaginez que les cigales aient une gamme de prédateurs qui passent également la majeure partie de leur vie dans le sol. Les cigales ont besoin de sortir de terre lorsque leurs prédateurs dorment.
Supposons qu’il existe des prédateurs avec des cycles de vie de 2, 3, 4, 5, 6, 7, 8 et 9 ans. Quelle est la meilleure façon de tous les éviter ?
Eh bien, comparez un cycle de vie de 13 ans et un cycle de vie de 12 ans. Lorsqu’une cigale avec un cycle de vie de 12 ans sort du sol, les prédateurs de 2 ans, 3 ans et 4 ans seront également hors du sol, car 2, 3 et 4 se divisent tous également en 12.
Lorsqu’une cigale avec un cycle de vie de 13 ans sort de terre, aucun de ses prédateurs ne sortira de terre, car aucun des 2, 3, 4, 5, 6, 7, 8 ou 9 ne se divise également en 13. Il en est de même pour 17.
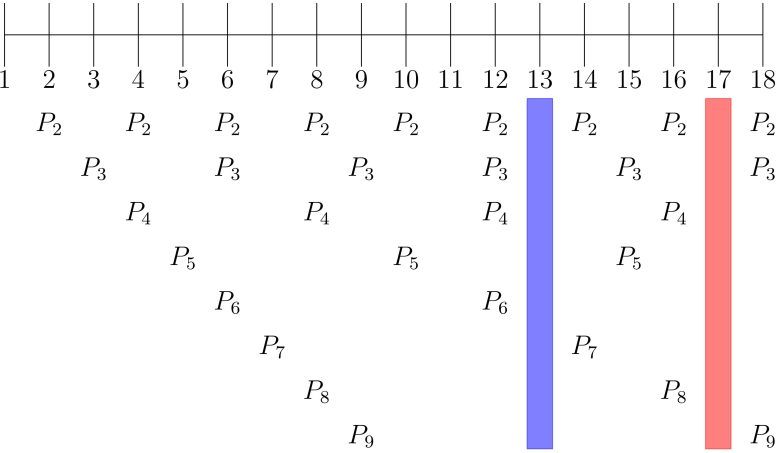
P1–P9 représentent les prédateurs cycliques. La droite numérique représente les années. Les lacunes mises en évidence montrent comment les cigales de 13 et 17 ans parviennent à éviter leurs prédateurs. Crédit : Sam Baron
Il semble ces cigales ont évolué pour exploiter des faits de base sur les nombres.
Création ou découverte ?
Une fois que nous commençons à chercher, il est facile de trouver d’autres exemples. De la forme de films de savon, à conception d’engrenage dans les moteurs, à l’emplacement et à la taille des interstices anneaux de Saturne, les mathématiques sont partout.
Si les mathématiques expliquent tant de choses que nous voyons autour de nous, alors il est peu probable que les mathématiques soient quelque chose que nous ayons créé. L’alternative est que les faits mathématiques sont découvert: pas seulement par les humains, mais par les insectes, les bulles de savon, les moteurs à combustion et les planètes.
Qu’en pensait Platon ?
Mais si nous découvrons quelque chose, qu’est-ce que c’est ?
L’ancien philosophe grec Platon avait une réponse. Il pensait que les mathématiques décrivent des objets qui existent réellement.
Pour Platon, ces objets comprenaient des nombres et des formes géométriques. Aujourd’hui, nous pourrions ajouter à la liste des objets mathématiques plus complexes tels que des groupes, des catégories, des fonctions, des champs et des anneaux.

Pour Platon, les nombres existaient dans un domaine séparé du monde physique.
Platon a également soutenu que les objets mathématiques existent en dehors de l’espace et du temps. Mais une telle vision ne fait qu’approfondir le mystère de la façon dont les mathématiques expliquent quoi que ce soit.
L’explication consiste à montrer comment une chose dans le monde dépend d’une autre. Si les objets mathématiques existent dans un domaine en dehors du monde dans lequel nous vivons, ils ne semblent pas capables de se rapporter à quoi que ce soit de physique.
Entrez dans le pythagoricisme
Les anciens pythagoriciens étaient d’accord avec Platon pour dire que les mathématiques décrivent un monde d’objets. Mais, contrairement à Platon, ils ne pensaient pas que les objets mathématiques existaient au-delà de l’espace et du temps.
Au lieu de cela, ils croyaient que la réalité physique est faite d’objets mathématiques de la même manière que la matière est faite d’atomes.
Si la réalité est faite d’objets mathématiques, il est facile de voir comment les mathématiques pourraient jouer un rôle dans l’explication du monde qui nous entoure.

Tarte pythagoricienne : le monde est fait de mathématiques et de matière. Crédit : Sam Baron
Au cours de la dernière décennie, deux physiciens ont monté des défenses importantes de la position pythagoricienne : le cosmologue suédo-américain Max Tegmark et physicien-philosophe australien Jane McDonnell.
Tegmark soutient que la réalité n’est qu’un grand objet mathématique. Si cela vous semble étrange, pensez à l’idée que la réalité est une simulation. Une simulation est un programme informatique, qui est une sorte d’objet mathématique.
Le point de vue de McDonnell est plus radical. Elle pense que la réalité est faite d’objets et d’esprits mathématiques. Les mathématiques sont la façon dont l’Univers, qui est conscient, en vient à se connaître.
je défends un vue différente: le monde a deux parties, les mathématiques et la matière. Les mathématiques donnent à la matière sa forme et la matière donne aux mathématiques leur substance.
Les objets mathématiques fournissent un cadre structurel pour le monde physique.
L’avenir des mathématiques
Il est logique que le pythagoricisme soit redécouvert en physique.
Au cours du siècle dernier, la physique est devenue de plus en plus mathématique, se tournant vers des domaines de recherche apparemment abstraits tels que la théorie des groupes et la géométrie différentielle dans le but d’expliquer le monde physique.
À mesure que la frontière entre la physique et les mathématiques s’estompe, il devient plus difficile de dire quelles parties du monde sont physiques et lesquelles sont mathématiques.
Mais il est étrange que le pythagoricisme ait été si longtemps négligé par les philosophes.
Je crois que c’est sur le point de changer. Le temps est venu d’une révolution pythagoricienne, qui promet de changer radicalement notre compréhension de la réalité.
Écrit par Sam Baron, professeur agrégé, Université catholique australienne.
Cet article a été publié pour la première fois dans La conversation.