Dans une nouvelle étude théorique FLEET publiée récemment dans Lettres d’examen physique, le soi-disant « pistolet fumant » dans la recherche du monopôle magnétique topologique – également connu sous le nom de courbure de Berry – a été trouvé.
La découverte est une percée dans la recherche d’effets topologiques dans les systèmes hors équilibre.
Le groupe, dirigé par le physicien et professeur agrégé de l’UNSW, Dimi Culcer, a identifié un effet Hall non conventionnel, entraîné par un champ magnétique dans le plan dans les systèmes de trous de semi-conducteurs qui peut être attribué exclusivement à la courbure de Berry.
Des effets topologiques améliorés permettront à l’électronique topologique à basse énergie d’être viable pour un fonctionnement à grande échelle à température ambiante, et soutiendront donc la feuille de route IEEE vers la durabilité future de l’électronique.
Isoler la réponse un moment décisif
« Isoler les réponses topologiques dans les « conducteurs réguliers » a été une tâche historiquement difficile», explique le chef de l’équipe de recherche A/Prof Dimi Culcer (UNSW). « Même si on pense que ces réponses topologiques sont omniprésentes dans les solides. »
Les réponses quantifiées, telles que les effets Hall quantique et spin-Hall quantique, fournissent une empreinte claire de la topologie, mais elles n’ont été observées que dans des systèmes unidimensionnels (1D) et sont intimement liées à l’existence d’états de bord.
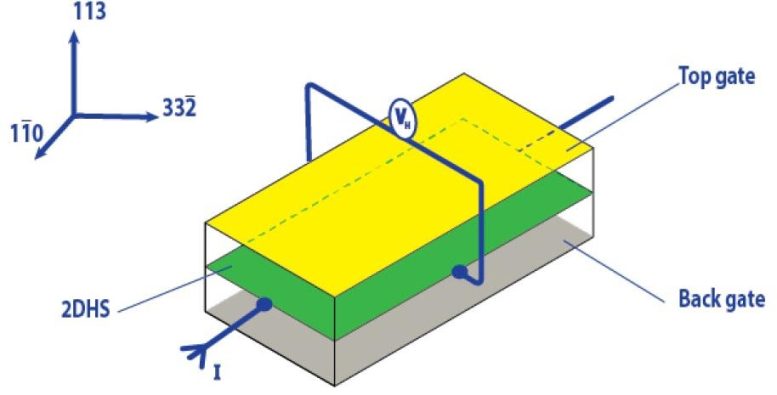
Un dispositif expérimental pour mesurer l’effet Hall conventionnel avec un champ magnétique perpendiculaire à la surface. Crédit : FLOTTE
Dans les conducteurs « réguliers », c’est-à-dire les systèmes 2D et 3D, il existe de nombreuses publications théoriques prédisant des contributions topologiques à, par exemple, l’effet Hall anormal, mais celles-ci n’ont jamais été observées sans ambiguïté dans une mesure de transport.
Il y a deux raisons principales à cela : (i) les électrons de spin-up et de spin-down apportent généralement des contributions opposées, et celles-ci s’annulent presque ; (ii) tout ce qui reste est submergé par le désordre.
Le nouveau document FLEET remédie à cette lacune de longue date en identifiant un système bidimensionnel dans lequel la courbure de Berry, et seulement la courbure de Berry, est responsable du signal Hall linéaire dans le champ magnétique appliqué dans le plan.
« Remarquablement, toutes les contributions aux troubles disparaissent : nous ne connaissons aucun autre système multidimensionnel dans lequel cela est vrai », déclare l’auteur principal, le doctorant de l’UNSW, James Cullen. “Sa mesure expérimentale est accessible à n’importe quel laboratoire de pointe dans le monde, c’est pourquoi nous nous attendons à un fort intérêt de la part des expérimentateurs.”
Courbure des baies, effet Hall anormal et matériaux topologiques
L’équipe de recherche a recherché la trace mathématique révélatrice appelée «courbure de Berry», qui peut être comprise si l’on pense au concept de transport parallèle qui apparaît régulièrement en géométrie et en relativité générale.
« Considérez un vecteur comme une flèche que nous plaçons quelque part sur la surface d’un objet solide », explique Dimi. « Maintenant, nous déplaçons la flèche en nous assurant qu’elle pointe toujours au même angle par rapport à la surface – c’est en fait comme un être humain marchant le long de la surface de la Terre. Nous ramenons finalement la flèche au point de départ après qu’elle ait fait le tour, et nous constatons qu’en général, elle pointe dans une direction différente – elle a tourné comme par magie d’un certain angle. La taille de cet angle est déterminée par la courbure de la surface. “
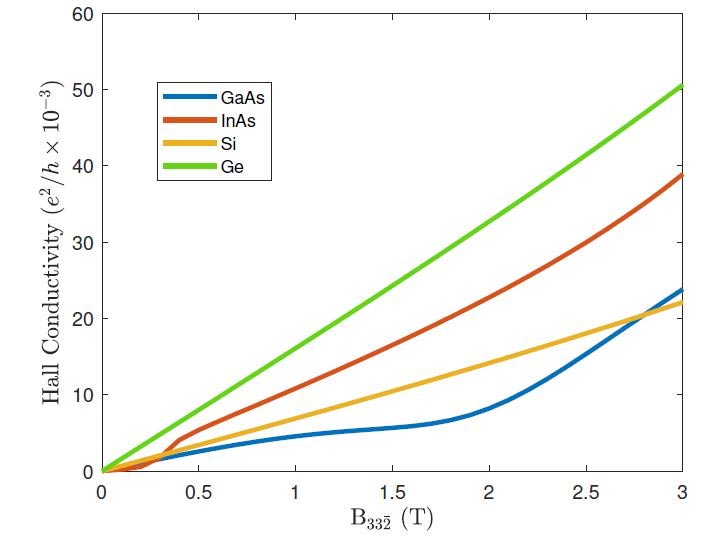
Réponse de la conductivité Hall au champ magnétique. Crédit : FLOTTE
En mécanique quantique, au lieu de vecteurs, nous avons des fonctions d’onde, mais nous pouvons décrire la dynamique en utilisant la même image, et la courbure est appelée la courbure de Berry.
L’angle de rotation est remplacé par la célèbre phase de Berry, du nom du physicien mathématicien Prof Sir Michael Berry, qui a formulé le problème dans les années 1980. Plus tard, en s’appuyant sur les travaux du lauréat du prix Nobel David Thouless, Qian Niu de l’UT Austin a montré que la courbure de Berry se comporte comme le monopole magnétique convoité, mais pas dans l’espace réel, mais plutôt dans l’espace de quantité de mouvement, qui est l’espace de la matière condensée que pensent les physiciens. dans.
La courbure de Berry entraîne des effets topologiques dans les systèmes hors équilibre, car lorsqu’un champ électrique est appliqué, un électron est accéléré, de sorte que sa quantité de mouvement change. Lorsque cela se produit, sa fonction d’onde change lentement, de la même manière que la “flèche” tourne en transport parallèle, et à la suite de cette rotation progressive, un courant transversal (Hall) est généré. Les relations d’Onsager, qui sont fondamentales pour la physique hors équilibre, disent que le courant de Hall ne dissipe pas d’énergie. Le cas extrême est l’effet Hall anormal quantique (QAHE), un effet quantique clé de la fonction des matériaux topologiques, dans lequel les courants de bord peuvent circuler avec une résistance électrique effectivement nulle.
(« Quantum » décrit la transition « étape » dans la résistance transversale (Hall) – c’est-à-dire qu’elle varie par étapes discrètes plutôt que progressivement – tandis que « anormal » fait référence à l’apparition du phénomène en l’absence de tout champ magnétique appliqué.)
Les chercheurs cherchent à améliorer QAHE afin de protéger le comportement topologique à des températures plus élevées, permettant une électronique topologique qui serait viable pour un fonctionnement à température ambiante.
« La réduction significative de la résistance électrique permise par le QAHE à température ambiante nous permettrait de réduire considérablement la consommation électrique des appareils électroniques », explique Dimi.
Référence : “Generating a topological anomalous Hall effect in a non-magnetic conduct: an in-planemagnetic field as a direct probe of the Berry curvature” par James H. Cullen, Pankaj Bhalla, E. Marcellina, AR Hamilton et Dimitrie Culcer, 21 juin 2021, Lettres d’examen physique.
DOI 10.1103/PhysRevLett.126.256601
En plus du soutien de l’Australian Research Council (programme des centres d’excellence), les auteurs reconnaissent le soutien du National Key Research and Development Program (Chine) et de la China Postdoctoral Science Foundation.



